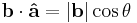Scalar projection
The scalar projection, also known as the scalar resolute or scalar component, of a vector 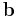 in the direction of a vector
in the direction of a vector 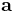 (or scalar projection of
(or scalar projection of 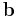 on
on 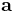 ) is given by:
) is given by:
where the operator  denotes a dot product,
denotes a dot product, 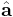 is the unit vector in the direction of
is the unit vector in the direction of 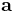 ,
, 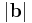 is the length of
is the length of 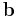 , and
, and  is the angle between
is the angle between 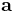 and
and 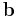 .
.
For an intuitive understanding of this formula, recall from trigonometry that 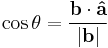 and simply rearrange the terms by multiplying both sides by
and simply rearrange the terms by multiplying both sides by 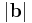 .
.
The scalar projection is a scalar, and is the length of the orthogonal projection of the vector 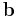 onto the vector
onto the vector 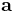 , with a minus sign if the direction is opposite.
, with a minus sign if the direction is opposite.
Multiplying the scalar projection by 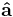 converts it into the vector projection, a vector.
converts it into the vector projection, a vector.